An array type for domain decomposition in Julia

MPI is the de-facto standard in the world of high-performance computing (HPC), and it can be a bit intimidating to learn at first. Julia is well-suited for HPC and it's quite easy to get up and running with MPI, thanks to the open source contributions to MPI.jl.

A few years ago I wrote a parallel Fortran code to simulate compressible flow. This code was parallelized using the domain decomposition method, where a large problem is split into many smaller problems that can be solved semi-independently. When I say semi-independently, I mean that these blocks or domains can be operated in parallel, but some amount of communication is still required. This is typically done using MPI to communicate data between domains. Neighbor information is exchanged using "halo" cells, which are fictitious grid cells that make communication simple. The tricky part of this is knowing what the neighbor domains are and how to efficiently pass data back and forth.

About a year ago, I wanted to learn Julia, so I converted this Fortran code (Cato) into Julia. Initially, the parallelization was accomplished using multi-threaded loops. This method of parallelization doesn't scale as well as domain decomposition, however. MPI is available in Julia, but I wanted to create a high-level library that facilitated halo exchange. MPIHaloArrays.jl is a new package that provides the MPIHaloArray array type (a subtype of AbstractArray), that does this communication for the user. While other existing libraries have similar decomposition functionality, such as MPIArrays.jl, PencilArrays.jl, and ImplicitGlobalGrid.jl , I wanted to create an array type specifically for this task. Each library only provides only a portion of the functionality I needed, so I decided to try creating a new one.

Domain decomposition splits a large problem into small subdomains that live on different MPI ranks. Stencil operations commonly used in solving PDEs require neighbor information, and this is done with halo cells along the edge of each subdomain. In 1D, it's a little easier to see compared to 2D and 3D; the image here shows how data must be exchanged for a halo size of 3:

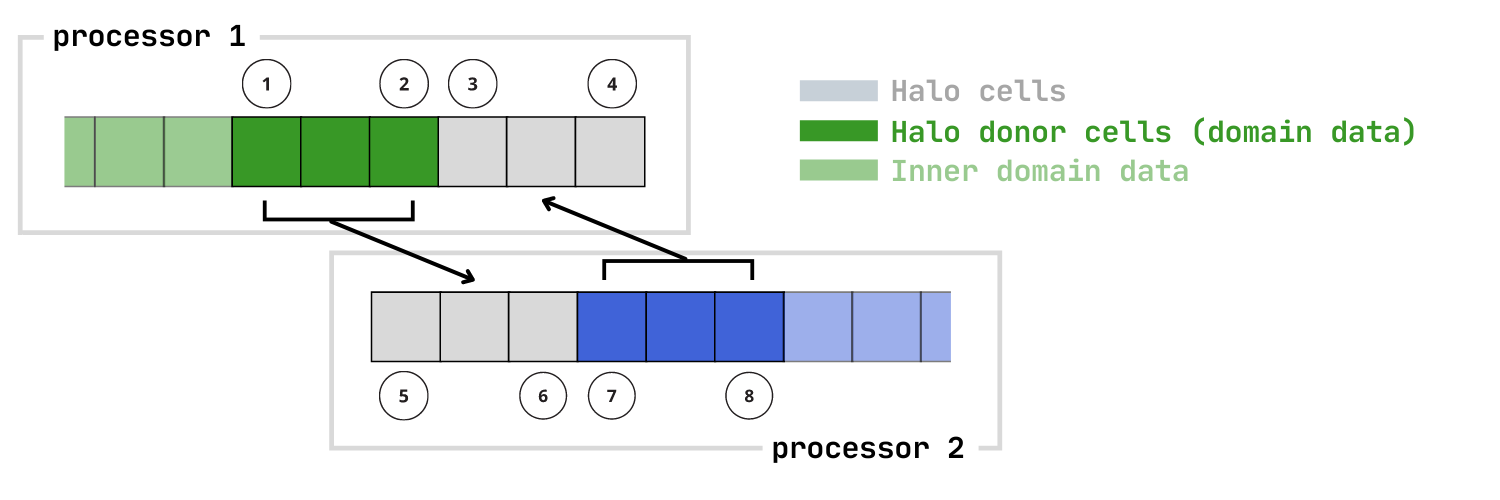
This can get quite complicated in 2D and 3D, especially when corner information is needed. MPIHaloArrays will do this communication for you in 1D, 2D, or 3D.

Features

• 1D, 2D, and 3D domain decomposition.

• Neighbor exchange with arbitrarily sized halo cell regions. Note, this is currently fixed across all dimensions.

• Communication is currently handled by MPI.ISend and MPI.IRecv underneath, but future versions will give the option for one-sided communication with MPI.Put and MPI.Get.

• Halo exchange can be orthogonal-only (e.g. [i+1,j,k]) , or it can include corners as well (e.g [i+1,j+1,k])

TODO

• GPU testing – I don’t currently have a local GPU to test this with, but future work will include GPU-aware MPI

• Fix the limitation of 1D, 2D, or 3D arrays. For example, an array U could have dimensions for [q,i,j], but halo exchanges are only done on i and j.

• Optimization of neighbor communication (caching, etc…)

• Finish one-sided implementation

Examples

Quickstart

using MPI, MPIHaloArrays

MPI.Init()
const comm = MPI.COMM_WORLD
const rank = MPI.Comm_rank(comm)
const nprocs = MPI.Comm_size(comm)
const root = 1

# Create a topology type the facilitates neighbor awareness and global size
topology = CartesianTopology(comm, 
                [4,2], # domain decompose in a 4x2 grid of ranks
                [false, false]) # no periodic boundaries
nhalo = 2

# Create some data on the local rank
local_data = rand(10,20) * rank
A = MPIHaloArray(local_data, topology, nhalo)
fillhalo!(A, -1)

# Perform halo exchange
updatehalo!(A)

# Or start with a large global array
B_global = rand(512,512)

# divide by rank and return B::MPIHaloArray
B_local = scatterglobal(B_global, root, nhalo, topology; 
                        do_corners = false) 
# do some work
# ....
updatehalo!(B_local)
# do some work
# ....

# and pull it back to the root rank
B_result = gatherglobal(B_local; root=root)

GC.gc()
MPI.Finalize()

2D Diffusion

See the example here in the GitHub repository.

Documentation

See the docs here